Question

A glider of mass 0.240 kg is on a frictionless, horizontal track, attached to a horizontal spring of force constant 6.00 N/m. Initially the spring (whose other end is fixed) is stretched by 0.100 m and the attached glider is moving at 0.400 m/s in the direction that causes the spring to stretch farther. What is the total mechanical energy (kinetic energy plus elastic potential energy) of the system?

Answer 1

`E_M=0.0492J`.

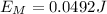Step-by-step explanation:

The mechanical energy of the system will be the kinetic energy plus the elastic potential energy:
`E_M=K+U_e`.

We know that the equation for the kinetic energy is
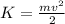`K=(mv^2)/(2)`, where m is the mass of the object and v its velocity.

We know that the equation for the elastic potential energy is
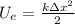`U_e=(k\Delta x^2)/(2)`, where k is the spring constant and
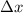`\Delta x` the compression (or elongation) respect to equilibrium.

So for our values we have:

`E_M=K+U_e=(mv^2)/(2)+(k \Delta x^2)/(2)=((0.24kg)(0.4m/s)^2)/(2)+((6N/m)(0.1m)^2)/(2)=0.0492J`.