Step-by-step explanation:
According to the Rydberg formula,
![(1)/(\lambda) = -R_(H)Z^(2) [(1)/(n^(2)_(i)) - (1)/(n^(2)_(f))]](https://img.qammunity.org/2020/formulas/chemistry/high-school/v5i61ixhs7yo4swr9jhqebpxaeprd6mbeu.png)
where,
 = wavelength
= wavelength
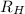 = Rydberg constant =
= Rydberg constant =
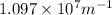
Z = atomic number (for He atomic number is 2)
 = 4,
= 4,
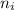 = 8
= 8
Hence, putting the given values into the above formula as follows.
![(1)/(\lambda) = -R_(H)Z^(2) [(1)/(n^(2)_(i)) - (1)/(n^(2)_(f))]](https://img.qammunity.org/2020/formulas/chemistry/high-school/v5i61ixhs7yo4swr9jhqebpxaeprd6mbeu.png)
=
![-1.097 * 10^(7) * (2)^(2) [(1)/((8)^(2)) - (1)/((4)^(2))]](https://img.qammunity.org/2020/formulas/chemistry/high-school/qcmlmmbnw3n8z458pbamib9su8otv8maln.png)
=
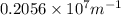
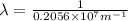
=
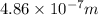
= 486 nm (as
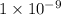 = 1 nm)
= 1 nm)
Thus, we can conclude that the Pickering series wavelength associated with the excited state is 486 nm.