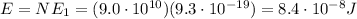Question

The emission line used for zinc determinations in atomic emission spectroscopy is 214 nm. If there are 9.00×1010 atoms of zinc emitting light in the instrument flame per second, what energy (in joules) must the flame supply during this time to achieve this level of emission?

Answer 1

`8.4\cdot 10^(-8)J`

Step-by-step explanation:

The energy emitted by a single photon is given by:

`E=(hc)/(\lambda)`

where

h is the Planck constant

c is the speed of light

`\lambda` is the wavelength of the photon

For the photons emitted by the zinc atoms,

`\lambda = 214 nm = 214 \cdot 10^(-9) m`

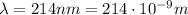
So the energy of a single photon emitted is

`E=((6.63\cdot 10^(-34))(3\cdot 10^8))/(214\cdot 10^(-9))=9.3\cdot 10^(-19)J`

And since the number of atoms is

`N=9.0\cdot 10^(10)`

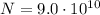
The total energy emitted will be

`E=NE_1 = (9.0\cdot 10^(10))(9.3\cdot 10^(-19))=8.4\cdot 10^(-8)J`