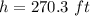Answer:
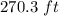
Explanation:
see the attached figure to better understand the problem
step 1
In the right triangle ADE
Find the value of h1
See the attached figure
h1=AD
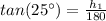
Solve for h1
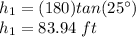
step 2
In the right triangle ABC
Find the value of h2
See the attached figure
h2=BC
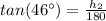
Solve for h2
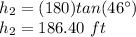
step 3
Find the height of the neighboring building
we know that
The height of the neighboring building is equal to
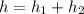
substitute the values
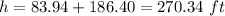
Round to the nearest tenth of a foot