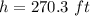Question

From her window, Carmella looks up to the top of a neighboring building at an angle of 46°. Her

angle of depression to the bottom of the building is 25°
The neighboring building is 180 feet away from the building Carmella is in.
How tall is the neighboring building?
round your answer to the nearest tenth of a foot

Answer 1

Answer: 270.3 ft

Step-by-step explanation: I took the test.

Answer 2

`270.3\ ft`

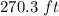
Explanation:

see the attached figure to better understand the problem

step 1

In the right triangle ADE

Find the value of h1

See the attached figure

h1=AD

`tan(25\°)=(h_1)/(180)`

Solve for h1

`h_1=(180)tan(25\°)\\h_1=83.94\ ft`

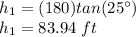
step 2

In the right triangle ABC

Find the value of h2

See the attached figure

h2=BC

`tan(46\°)=(h_2)/(180)`

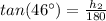
Solve for h2

`h_2=(180)tan(46\°)\\h_2=186.40\ ft`

step 3

Find the height of the neighboring building

we know that

The height of the neighboring building is equal to

`h=h_1+h_2`

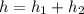
substitute the values

`h=83.94+186.40=270.34\ ft`

Round to the nearest tenth of a foot

`h=270.3\ ft`