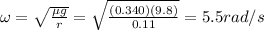Question

A coin rests 11.0 cm from the center of a turntable. The coefficient of static friction between the coin and turntable surface is 0.340. The turntable starts from rest at t = 0 and rotates with a constant angular acceleration of 0.820 rad/s2. (b) At what angular speed (ω) will the coin start to slip?

Answer 1

5.5 rad/s

Step-by-step explanation:

The friction between the coin and the turntable provides the centripetal force that keeps the coin in circular motion. Therefore, we can write:

`\mu mg = m\omega^2 r`

where

`\mu = 0.340` is the coefficient of friction

m is the mass of the coin

`g=9.8 m/s^2` is the acceleration of gravity

`\omega` is the angular speed

r is the distance of the coin from the centre of rotation

In this problem,

r = 11.0 cm = 0.11 m

The coin starts to slip when the centripetal force becomes larger than the maximum frictional force:

`m\omega^2 r > \mu m g`

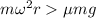
Solving for
`\omega`, we find the angular speed at which this happens:

`\omega = \sqrt{(\mu g)/(r)}=\sqrt{((0.340)(9.8))/(0.11)}=5.5 rad/s`