Question

A 3.57 kg block is drawn at constant speed 4.06 m along a horizontal floor by a rope exerting a 7.68 N force at angle of 15deg. above the horizontal. Compute (a) the work done by the rope on the block, and (b) the coefficient of kinetic friction between block and floor.

Answer 1

Step-by-step explanation:

Given

mass of block=3.57 kg

distance =4.06 m

Force on rope(F)=7.68 N

inclination \theta =15

cos component of rope will do work on block

`W=F\cdot s`

`W=F s \cos 15`

`W=7.68* 4.06* \cos 15`

W=30.11 J

(b)constant speed implies that Force exerted by rope is being balanced by friction in horizontal direction

`F\cos \theta =f_r`

`f_r=\mu N`

`f_r=\mu (mg-F\sin \theta )`

`f_r=\mu 33.006`

`7.418=\mu * 33.006`

`\mu =0.22`

Answer 2

Step-by-step explanation:

It is given that,

Mass of the block, m = 3.57 kg

It is drawn to a distance of, d = 4.06 m

Horizontal force acting on the rope, F = 7.68 N

Angle above horizontal,
`\theta=15^(\circ)`

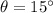
(A) The work done by the rope on the block is W. It can be calculated as :

`W=Fd\ cos\theta`

`W=7.68* 4.06\ cos(15)`

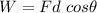
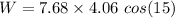
W = 30.11 joules

(b) Let
`\mu` is the coefficient of kinetic friction between block and floor. According to the free body diagram of the given problem. At equilibrium,

`Fcos\theta=\mu(mg-Fsin\theta)`

`\mu=(Fcos\theta)/((mg-Fsin\theta))`

`\mu=(7.68* cos(15))/((3.57* 9.8-7.68* sin(15)))`

`\mu=0.22`

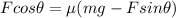
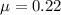
Hence, this is the required solution.