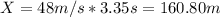Question

Small-plane pilots regularly compete in "message drop" competitions, dropping heavy weights (for which air resistance can be ignored) from their low-flying planes and scoring points for having the weights land close to a target. A plane 55m above the ground is flying directly toward a target at 48m/s .A)At what distance from the target should the pilot drop the weight?Express your answer to two significant figures and include the appropriate units.

Answer 1

It should be dropped from 160.80m

Step-by-step explanation:

To calculate the time it takes the weight to reach the ground from 55m we need to consider that the only acceleration applied to it is the gravity, the height at any time t can be calculate as:

`Y=Y_(0)+Vy_(0)*t-1/2*g*t^(2)`

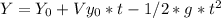
If we consider that it starts from
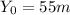`Y_(0)=55m` to reach Y=0, and that the initial velocity on the vertical axis equals zero:

`0=55m-1/2*g*t^(2)`

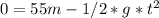
solving for t:

`t=\sqrt{(55m*2)/(g) } =\sqrt{(110m)/(9.8m/s^(2) ) }=3.35s`

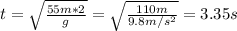
Now to calculate the horizontal distance from the target:

`X=X_(0)+Vx_(0)*t-1/2*a*t^(2)`

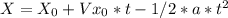
We have to consider that:

It will travel from
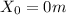`X_(0)=0m` (we set the reference on the dropping point so the result X will be de needed distance;

As the air resistance can be ignored there is no force on the horizontal direction, a=0;

The starting velocity
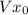`Vx_(0)` is the same of the plane velocity

It will be traveling for a time t calculated before;

replacing this on the equation:

`X=48m/s*3.35s=160.80m`