Question

A summer camp cookout is planned for the campers and their families. There is room for 525 people. Each adult costs $9, and each camper costs $5. There is a maximum budget of $1,200. Write the system of inequalities to represent this real-world scenario, where x is the number of adults and y is the number of campers.

Answer 1

x+y < = 525

9x+5y < = 1200

Explanation:

Answer 2

The System of Inequalities in this real-world scenario is:

x+y < = 525

9x+5y < = 1200

Explanation:

In this question we are asked to to write a system of inequalities, thus a system of relating two variables, where the relationship will be of the form either greater > or less < or equal.

Given Information:

→ Maximum number possible in the summer camp: 525

→ People attending are Adults (lets call them
`x` and Campers (lets call them
`y`)

→ Ticket Cost for Adults is $9

→ Ticket Cost for Campers is $5

→ Maximum budget available for both Adults and Campers is $1200

From these information we can obtain 2 Inequalities to define our system of equation.

The first inequality will be with respect to the Maximum Number of People possible which reads as:

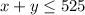`x+y\leq 525` [sum of adults and campers should be less or equal to maximum number of people possible]

The second will be with respect to the Maximum Budget available which reads as:

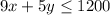`9x+5y\leq 1200` [sum of the cost per ticket for adults and campers should be less or equal to maximum budget available]

Thus the System of Inequalities in this real-world scenario is:

`x+y\leq 525\\9x+5y\leq 1200`

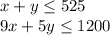
Which if solved can give us the values for
`x` and
`y`, thus the number of adults and numbe of campers attedning the summer camp.