Question

A brick of mass 1.15 kg is attached to a thin (massless) cable and whirled around in a circle in a vertical plane. The circle has a radius of 1.44 m. The cable will break if the tension exceeds 43.0 Newtons. What is the maximum speed the brick can have at the bottom of the circle before the cable will break?

Answer 1

Step-by-step explanation:

It is given that,

Mass of the brick, m = 1.15 kg

Radius of the circle, r = 1.44 m

The cable will break if the tension exceeds 43.0 N

Let v is the maximum sped can have at the bottom of the circle before the cable will break. At the bottom of the circle, the net force is equal to the centripetal force along with the weight of the brick. So,

`T=(mv^2)/(r)+mg`

`(T)/(m)-g=(v^2)/(r)`

`v=\sqrt{((T)/(m)-g)r}`

`v=\sqrt{((43)/(1.15)-9.8)* 1.44}`

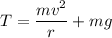
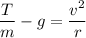
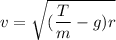
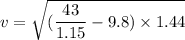
v = 6.30 m/s

So, the maximum speed of the brick at the bottom of the circle before the cable will break is 6.3 m/s. Hence, this is the required solution.