Question

A box sits on a horizontal wooden ramp. The coefficient of static friction between the box and the ramp is 0.34. You grab one end of the ramp and lift it up, keeping the other end of the ramp on the ground. What is the angle between the ramp and the horizontal direction when the box begins to slide down the ramp?

Answer 1

The angle between the ramp and the horizontal direction is 18.7°.

Step-by-step explanation:

Given that,

Coefficient of static friction = 0.34

According to figure,

The normal force is equal to the y component of weight of the box

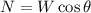`N=W\cos\theta`....(I)

We need to calculate the angle between the ramp and the horizontal direction

Using frictional force

`f_(\mu)=\mu\ N`

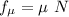
Put the value of frictional force and N into the formula

`W\sin\theta=0.34*W\cos\theta`

`\tan\theta=0.34`

`\theta=\tan^(-1)(0.34)`

`\theta=18.7^(\circ)`

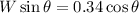
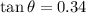
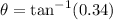
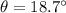
Hence, The angle between the ramp and the horizontal direction is 18.7°.