In the context of B being the midpoint of AC, the proof demonstrates that
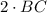 equals AB, highlighting the relationship between the segments in a scenario where B is the midpoint.
equals AB, highlighting the relationship between the segments in a scenario where B is the midpoint.
In the given scenario where B is the midpoint of AC, we aim to prove that
 .
.
By the definition of a midpoint, BC is equal to BA (segment addition postulate).
Now, considering the entire segment AC, which is composed of two equal parts (AB and BC), we can express AC as
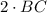 .
.
Substituting the earlier established equality BC = BA into this expression, we get
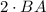 , which is equivalent to AB.
, which is equivalent to AB.
Thus,
 , confirming the assertion that in a segment where B is the midpoint, the double of one of its segments equals the other segment.
, confirming the assertion that in a segment where B is the midpoint, the double of one of its segments equals the other segment.