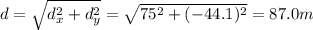a) horizontal: 25.0 m/s, vertical: -19.6 m/s
As the rock is thrown horizontally, it follows a parabolic motion (projectile motion), where:
- The horizontal motion is a uniform motion, with constant velocity
- The vertical motion is a uniformly accelerated motion, with constant acceleration
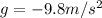 towards the ground (we take upward as positive direction, so the acceleration is negative)
towards the ground (we take upward as positive direction, so the acceleration is negative)
We said that the horizontal velocity is constant, so it remains equal to the velocity at which the rock was thrown from the cliff, therefore
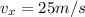
And this is also the value of the horizontal velocity at t = 2.0 s.
Instead, the vertical velocity follows the equation
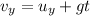
where:
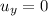 is the initial vertical velocity
is the initial vertical velocity
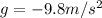 is the acceleration of gravity
is the acceleration of gravity
t = 2.0 s is the time
Substituting,
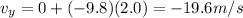
b) 38.6 m/s at
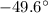
In order to find the velocity at 3.0 s, we should find its horizontal and vertical components at that time first.
As we said, the horizontal velocity is constant:
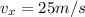
while the vertical velocity is given by
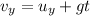
And substituting t = 3.0 s,

The magnitude of the velocity at 3.0 s therefore is

While the direction is given by
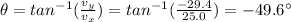
where the negative sign means the angle is below the horizontal.
c) 87.0 m
In order to find the displacement, we should find the horizontal and vertical distance travelled by the rock in 3.0 s.
Along the horizontal direction, the motion is uniform, so the horizontal distance travelled is
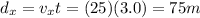
While the distance travelled along the vertical direction is given by the equation

And substituting t = 3.0 s,
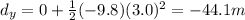
So, the displacement of the rock after 3.0 s is