Answer:
11 grams
Step-by-step explanation:
To find the remaining mass of radium-226, you need to use the half-life formula:
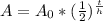
In this formula,
-----> A = remaining mass (g)
-----> A₀ = initial mass (g)
-----> t = time passed (yrs)
-----> h = half-life (yrs)
You can plug the given values into the formula and solve to find the remaining mass (A).
A = ? g t = 4,800 yrs
A₀ = 88 g h = 1,600 yrs
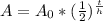 <----- Half-life formula
<----- Half-life formula
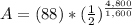 <----- Insert values
<----- Insert values
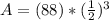 <----- Divide 1,600 from 4,800
<----- Divide 1,600 from 4,800
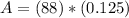 <----- Raise
<----- Raise
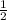 to the power of 3
to the power of 3
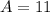 <----- Multiply 88 and 0.125
<----- Multiply 88 and 0.125