2 Answers

Pacemaker · Answer 1 · 2020-04-23T13:16:46+0000

You can observe that every next term is computed by adding 4 to the previous one.

This implies that the difference between consecutive terms is always 4, and this is an arithmetic sequence.

In order to find the explicit equation, we can explore the pattern:

$a_1 = -1 = -1+4\cdot 0$

$a_2 = 3 = -1+4\cdot 1$

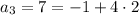
$a_3 = 7 = -1+4\cdot 2$

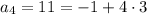
$a_4 = 11 = -1+4\cdot 3$

So, as you can see, we have

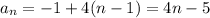
a_n = -1+4(n-1) = 4n-5

If 109 is a term of the sequence, there must exist a natural number n such that

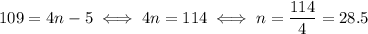
$109 = 4n-5 \iff 4n = 114 \iff n = (114)/(4) = 28.5$

So, 109 is not a term of the sequence.

Please log in or register to add a comment.