ELIMINATION:
You can multiply the second equation by 2:
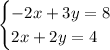
And then add the two equations:
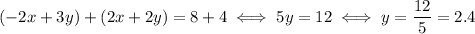
And we deduce
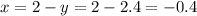
SUBSTITUTION:
From the second equation, we derive
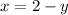
Plug this expression for x in the first equation:
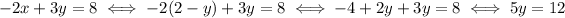
And from here you proceed in the same way as above.