Answer:
BD=46
Explanation:
In the given question we have a Triangle Δ BCD, that is intersected by CA, and dividing Δ BCD in half. The line CA creates two new Right Triangles denoted as Δ BCA and Δ DCA.
Right Triangles are characterized by one orthogonal angle that is always 90° and two more angles (lets call them ∠x and ∠y) so that:
∠x + ∠y + ∠90° = 180°
In this case we can start analysing each Right triangle individually at first. As such, we shall use the Pythagorian Theorem which relates all three sides of a Right triangle as follow:
In Δ BCA:
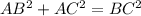 Eqn(1).
Eqn(1).
In Δ DCA:
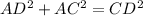 Eqn(2).
Eqn(2).
which means that the Hypotenuse Length Squared (in this case BC and CD) are equal to the sum of the remaining two sides length's squared (in this case AB and AC for Δ BCA and similarly AD and AC for Δ DCA)
In the question it is also given that BC = CD which implies that Eqn(1) = Eqn(2) as follow:
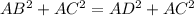
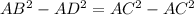 Gathering similar sides/terms
Gathering similar sides/terms
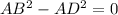 AC cancels out
AC cancels out
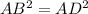 Transfering AD on the right hand side
Transfering AD on the right hand side
AB=AD
We also know that
 , hence from our result above we can say that
, hence from our result above we can say that
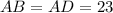 Eqn(3)
Eqn(3)
Finally since
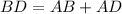 , as shown on the Schematic Attached and along with Eqn(3) we have
, as shown on the Schematic Attached and along with Eqn(3) we have
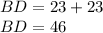
There are other methods of proving such result using Pythagorian Theorem, Angles Relations and/or Triangle Sides/Comparison.