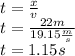Question

You throw a ball with a speed of 25.0 m/s at an angle of 40.0â—¦ above the horizontal directly toward a wall. The wall is 22.0 m from the release point of the ball. How long does the ball take to reach the wall?

Show Options
A.11.15 s
B.11.5 s
C.1.115 s
D.1.15 s

Answer 1

The horizontal speed is going to be the cosine of the given speed, therefore, the horizontal speed is 19.15 m/s. To find the time, divide the 22 m distance by the velocity. This results in 1.131 seconds, which is in between C and D.

Answer 2

D.1.15 s

Step-by-step explanation:

When we decompose the velocity into two perpendicular components, the total vector and its components form a right triangle. Therefore, these components will be given by:

`cos\theta=(v_x)/(v)\\v_x=vcos\theta(1)\\sin\theta=(v_y)/(v)\\v_y=vsin\theta`

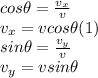
Using (1), we calculate the horizontal speed of the ball:

`v_x=25(m)/(s)cos(40^\circ)\\v_x=19.15(m)/(s)`

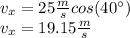
Recall that
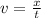`v=(x)/(t)`, solving for t:

`t=(x)/(v)\\t=(22m)/(19.15(m)/(s))\\t=1.15s`