Question

What is the vertex of the quadratic function f(x) = (x – 8)(x + 2)?

Answer 1

The vertex is (3,-25)

Explanation:

Quadratic Function has the form:

`f(x)=ax^2+bx+c`

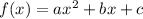
Lets use distributive property [a(b+c)=ab+ac] to make the equation given into the vertex form. Thus, we have:

`f(x)=(x-8)(x+2)\\f(x)=x^2+2x-8x-16\\f(x)=x^2-6x-16`

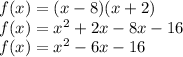
Thus,

a = 1

b = -6

c = -16

The x coordinate of vertex is given as:

`x=-(b)/(2a)`

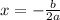
Putting the points, we have:

`x=-(-6)/(2(1))=3`

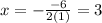
Putting x = 3 into the function, we get y-value of vertex:

`f(x)=(x-8)(x+2)\\f(x)=(3-8)(3+2)\\f(x)=(-5)(5)\\f(x)=-25`

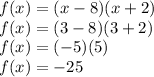
The vertex is (3,-25)