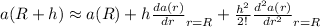Answer:
g(h) = g ( 1 - 2(h/R) )
*At first order on h/R*
Step-by-step explanation:
Hi!
We can derive this expression for distances h small compared to the earth's radius R.
In order to do this, we must expand the newton's law of universal gravitation around r=R
Remember that this law is:
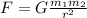
In the present case m1 will be the mass of the earth.
Additionally, if we remember Newton's second law for the mass m2 (with m2 constant):
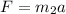
Therefore, we can see that
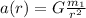
With a the acceleration due to the earth's mass.
Now, the taylor series is going to be (at first order in h/R):
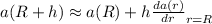
a(R) is actually the constant acceleration at sea level
and
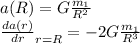
Therefore:

Consider that the error in this expresion is quadratic in (h/R), and to consider quadratic correctiosn you must expand the taylor series to the next power: