Question

18. A set of data has a sample mean of 65.4 and a standard deviation of 1.2. If the sample size is 45, what is the 99% confidence interval of this data?

A. 65.10 and 65.70
B. 65.33 and 65.47
C. 65.05 and 65.75
D. 64.94 and 65.86

Answer 1

the answer is, 64.94 and 65.86

Explanation:

Answer 2

Given:

Sample mean = 65.4

Standard deviation = 1.2

Sample size = 45

Confidence level = 99%

To find:

The confidence interval.

Solution:

The formula for confidence interval is

`CI=\overline{x}\pm z^*(s)/(√(n))`

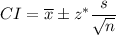
where,
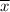`\overline{x}` is sample mean, z* is confidence value, s is standard deviation and n is sample size.

Confidence value or z-value at 99% = 2.58

Putting the given in the above formula, we get

`CI=65.4\pm 2.58* (1.2)/(√(45))`

`CI=65.4\pm 0.46`

`CI=65.4-0.46\text{ and }CI=65.4+0.46`

`CI=64.94\text{ and }65.86`

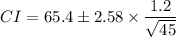
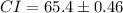
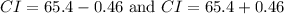
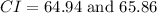
Therefore, the correct option is D.