Answer:
The correct option is D)
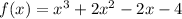 .
.
Explanation:
Consider the provided cubic function.
We need to find the equation having zeros: Square root of two, negative Square root of two, and -2.
A "zero" of a given function is an input value that produces an output of 0.
Substitute the value of zeros in the provided options to check.
Substitute x=-2 in
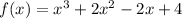 .
.
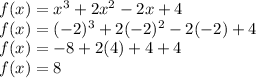
Therefore, the option is incorrect.
Substitute x=-2 in
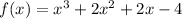 .
.
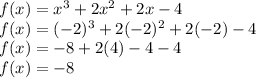
Therefore, the option is incorrect.
Substitute x=-2 in
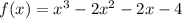 .
.
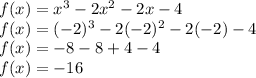
Therefore, the option is incorrect.
Substitute x=-2 in
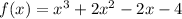 .
.
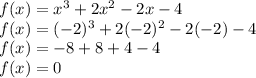
Now check for other roots as well.
Substitute x=√2 in
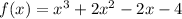 .
.
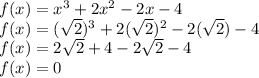
Substitute x=-√2 in
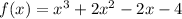 .
.
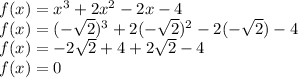
Therefore, the option is correct.