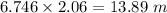Question

A cliff diver positions herself on the edge of a cliff that angles downward towards the edge. The length of the top of the cliff is 41.0 m and the angle of the cliff is 20.0 degrees below the horizontal. The cliff diver runs toward the edge at a constant speed, and reaches the edge with a time of 5.71 s. after running straight off the edge without jumping up, the diver falls h=26.0 m before hitting the water.After leaving the edge of the cliff how much time does the diver take to get to the water?How far horizontally does the diver travel from the cliff face before hitting the water?Remember that the angle is at a downward slope to the right.

Answer 1

Time taken is 2.06 s

The horizontal distance traveled is 13.89 m

Solution:

As per the question:

Length of the cliff-top, l = 41.0 m

Angle of the cliff,
`\theta = 20.0^(\circ)`

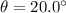
Time taken by the diver to reach the edge, t' = 5.71 s

Height, H = 26.0 m

Now,

Speed of the diver at the edge, u =
`(l)/(t') = (41.0)/(5.71) = 7.18\ m/s`

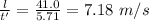
Also, vertical component of the initial speed of the diver, u' =
`usin\theta = 7.18sin20.0^(\circ) = 2.455\ m/s`

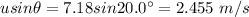
The time taken by the diver to reach the water is given by the second eqn of motion for vertically downward motion:

`h = u't + (1)/(2)gt^(2)`

`26 = 2.455t + (1)/(2)* 9.8* t^(2)`

`4.9t^(2) + 2.455t - 26 = 0`

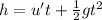
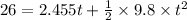
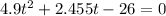
Solving the above quadratic eqn, we get:

t = 2.06, - 2.56

Since, time can't be negative

Thus

t = 2.06 s

Now,

Speed in the horizontal direction, v =
`ucos\theta = 7.18cos20.0^(\circ) = 6.746\ m/s`

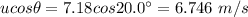
The horizontal distance traveled by the diver is given by:

x = vt =
`6.746* 2.06 = 13.89\ m`