Question

A 25.0 steel wire and a 50.0 copper wire are attached end to end and stretched to a tension of 145 . Both wires have a radius of 0.450 . and their densities are 7.86 10 / for the steel and 8.92 10 / for the copper. (Note that these are mass densities, mass per unit volume, NOT linear mass densities, mass per unit length.) How long does a wave take to travel from one end to the other of the combination wire?

Answer 1

T= 0.45 sec

Step-by-step explanation:

Given data:

length of steel wire = 25 m

length of copper wire is 50 m

tension = 145 N

STEEL AND COPPER WIRE diameter = 0.450

density of steel
`= 7.86* 10^(3) kg/m3`

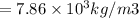
density of copper
`= 8.92* 10^3 kg/m3`

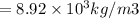
we know that speed of waves is calculated as

`V =\sqrt{(T)/(U)}`

`U =  \rho * A`

`V_(STEEL) = \sqrt{(145)/(8.92* 10^3 * \pi (0.45* 10^(-3))^2)}`

`V_(STEEL) = 160 m/s`

`V_(copper) = \sqrt{(145)/(7.86* 10^3 * \pi (0.45* 10^(-3))^2)}`

`V_(copper) = 170 m/s`

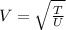
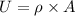
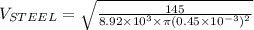
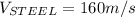
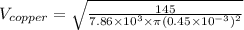
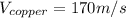
time travel by wave from one end to other

`=(l_s)/(v_s) + (l_c)/(v_c)`

`= (25)/(160) + (50)/(170)`

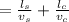
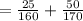
T= 0.45 sec