Question

1. A 700 kg satellite is in orbit 2.4 x 106 meters from the center of the Earth. What is the force of

gravity on the satellite?​

Answer 1

`4.8 \cdot 10^4 N`

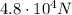
Step-by-step explanation:

The force of gravity acting on the satellite is given by:

`F=(GMm)/(r^2)`

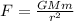
where

G is the gravitational constant

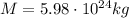`M=5.98\cdot 10^(24) kg` is the Earth's mass

m is the mass of the satellite

r is the distance of the satellite from the Earth's centre

Here we have

m = 700 kg

`r=2.4\cdot 10^6 m`

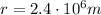
Substituting into the equation, we find:

`F=((6.67\cdot 10^(-11))(5.98\cdot 10^(24))(700))/((2.4\cdot 10^6)^2)=4.8 \cdot 10^4 N`

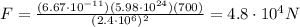
Note that the distance mentioned in the problem (2.4 x 10^6 meters) is not realistic, since it is less than the radius of the Earth (6.37 x 10^6 meters).