Question

1. f(x) = (x + 2)2 + 1

Direction of opening:
Vertex:
Axis of Symmetry:
y-intercept:
Buddy point:
What is the direction of opening

Answer 1

1) Direction of opening: upward

2) Vertex is the point (-2,1)

3) Axis of Symmetry: x=-2

4) y-intercept: point (0,5)

5) Buddy point:
`x_1=-2+i` and
`x_2=-2-i`

Explanation:

we have

`f(x)=(x+2)^(2)+1`

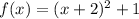
This is the equation of a vertical parabola in vertex form

The general equation of a vertical parabola in vertex form is equal to

`f(x)=a(x-h)^(2)+k`

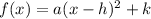
where

(h,k) is the vertex

a is the coefficient of variable x^2

If a > 0 -----> the parabola open upward and the vertex is a minimum

If a < 0 -----> the parabola open downward and the vertex is a maximum

The axis of symmetry is equal to the x-coordinate of the vertex

x=h

In this problem we have

`f(x)=(x+2)^(2)+1`

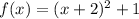
The vertex is the point (-2,1)

The coefficient a is equal to a=1

so

a> 0

the parabola open upward and the vertex is a minimum

The axis of symmetry is

x=-2

Find out the y-intercept

Remember that the y-intercept is the value of y when the value of x is equal to zero

For x=0

`f(x)=(0+2)^(2)+1`

`f(x)=5`

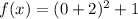
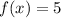
The y-intercept is the point (0,5)

Find the x-intercepts

Remember that the x-intercept is the value of x when the value of y is equal to zero

so

For f(x)=0

`0=(x+2)^(2)+1`

`(x+2)^(2)=-1`

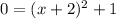
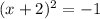
The roots are complex

take square root both sides

`(x+2)=(+/-)√(-1)`

Remember that

`i=√(-1)`

`x=-2(+/-)i`

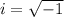
The solutions are

`x_1=-2+i`

`x_2=-2-i`

therefore

1) Direction of opening: upward

2) Vertex is the point (-2,1)

3) Axis of Symmetry: x=-2

4) y-intercept: point (0,5)

5) Buddy point:
`x_1=-2+i` and
`x_2=-2-i`