Answer with Step-by-step explanation:
We are given that f(x)=

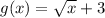
a.We have to show that
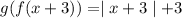
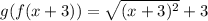
When we remove square root then we take plus minus therefore we write in modulus.
Therefore,

Hence, proved.
b.We have to find that
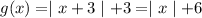
Substitute x=-3
Then, we get
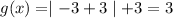
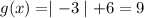
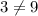
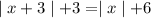 for
for
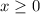
But,
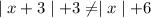 for x<0
for x<0
Hence,
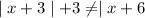 for all x.
for all x.