Answer:
x=5,y=1 and z=-2
Explanation:
We are given that system of equation
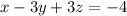 (I equation)
(I equation)
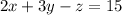 (II equation )
(II equation )
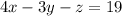 (III equation )
(III equation )
Equation II multiply by 3 then add with equation I
Then, we get
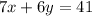 ....(Equation IV)
....(Equation IV)
Subtract equation II from equation III then we get
 (equation V)
(equation V)
Adding equation IV and equation V then, we get
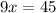

Substitute x=5 in equation V then, we get
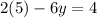
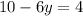
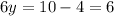
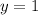
Substitute x=5 and y=1 in equation then, we get
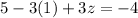
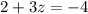
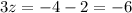
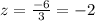
Hence, the solution for the given system of equation is given by
x=5,y=1 and z=-2