Question

The area and circumference of a circle of radius r are given by A(r) = πr2 and C(r) = 2πr. Suppose we increase

the radius of a sphere by 0.001 units from r to r + 0.001.
a. Use the binomial theorem to write an expression for the increase in area volume A(r + 0.001) − A(r) as a
sum of three terms.
b. Write an expression for the average rate of change of the area as the radius increases from r to r + 0.001.
c. Simplify the expression in part (b) to compute the average rate of change of the area of a circle as the radius
increases from r to r + 0.001.
d. What does the expression from part (c) resemble?
e. Why does it make sense that the average rate of change should approximate the area of a circle? Think about
the geometric figure formed by A(r + 0.001) − A(r). What does this represent?
f. How could we approximate the area of the shell using circumference? And the average rate of change for the
area?
g. Find the difference between the average rate of change of the area and C(r) when r = 1.

Answer 1

Please see the result step by step, as follows:

Explanation:

Let us start by writing down both expressions for an given increased radius

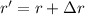`r'=r+\Delta r`, where the second term is the radius increment:

• Increased area:
  `A'=\pi (r+\Delta r)^(2) =\pi(r^2+(\Delta r)^2+2r\Delta r)=\pi r^2+ \pi(\Delta r)^2+2\pi r\Delta r`
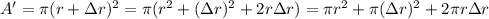
• Increased circumference (length):
  `C'=2 \pi (r + \Delta r) = 2 \pi r + 2 \pi \Delta r`

Here, he just used the binomial theorem, set as:

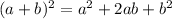`(a+b)^2=a^2+2ab+b^2`, applied to the sum of the new, increased ratio.

a. So, for an increment of
`\Delta r = 0.001`,

`\Delta A(\Delta r = 0.001) = A(r+0.001) - A(r) = (\pi r^2+ \pi(\Delta r)^2+2\pi r \Delta r) - \pi r^2= \pi(\Delta r)^2+2\pi r \Delta r = \pi(0.001)^2+0.002 \pi r = \pi (0.00001 + 0.002 r)`

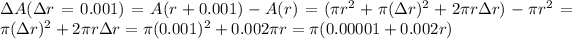
It is a two terms expression, not three.

b. The average expression is built by the increment of area A divided by the increment of radius:

`ave(\Delta A) = (A(r+ \Delta r) - A(r))/((r+\Delta r) - r) = (\Delta A)/(\Delta r) = \pi ( ((\Delta r)^2+2 r \Delta r ) )/(\Delta r)=\pi (\Delta r + 2r)`.

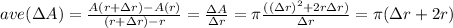These values have to be specified for
`0< \Delta r < 0.001`.

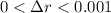Another condition is needed for this step:
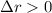`\Delta r > 0`. Otherwise, for
`\Delta r = 0`,
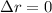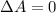`\Delta A = 0` (trivial).

c. From b., applyng
`\Delta r = 0.001`,

`ave(\Delta A) = \pi (0.001 + 2r)`.

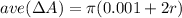d. This is expression results in a linear expression. The first term is similar to a circumference whose radius is half of 0.001; the second one is similar to the circumference's original expression, due to its second term,
`2 \pi r`.

e. This makes sense since the geometric figure formed is, in fact, a circular crown, whose width is
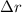`\Delta r` and whose approximate lentgh is
`r`.

f. An approximate expression for the "shell" (our new circular crown) can be built by multiplying a circumference (length) by its width (
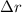`\Delta r`), thus resulting in an area value.

• 
  `\Delta A* =2 \pi r \Delta r`

This is an approximation, not the exact expression that we calculated above; remember:

• 
  `\Delta A = \pi ((\Delta r)^2 + 2r \Delta r))`.

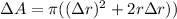So, we just neglected the first, smaller and negligible term,
`\pi (\Delta r)^2`

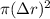
g. As stated in d.,
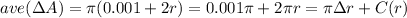`ave(\Delta A) = \pi (0.001 + 2r) = 0.001 \pi + 2 \pi r = \pi \Delta r + C(r)`. As you can see here, the average rate of change of the area and C(r) differ by the latter expression's first term, so:

• 
  `ave(\Delta A)(r=1) = \pi (0.001 + 2) = 2.001 \pi`