Question

Use the binomial theorem to expand the following binomial expressions.

a. (x + y)4
b. (x + 2y)4
c. (x + 2x)4
d. (x − y)4
e. (x − 2xy)4

Answer 1

Explanation:

a.

1

1 2 1

1 3 3 1

1 4 6 4 1

(x+y)^4=1 x^4+4x³y+6 x²y²+4xy3 +1y^4

=x^4+4x³y+6x²y2+4xy³+y^4

or

(x+y)^4=4c0 x^4+4c1 x³y+4c2x²y²+4c3xy³+4c4y^4

4c0=4c4=1

4c1=4/1=4

4c2=(4×3)/(2×1)=6

4c3=4c1=4

so \[(x+a)^4=x^4+4x³y+6x²y²+4xy³+y^4\]

b.

\[(x+2y)^4=x^4+4x³(2y)+6x²(2y)^2+4x(2y)³+(2y)^4\]

=x^4+8x³y+24x²y²+32xy³+16y^4

c.

(x+2x)^4=(3x)^4=81x^4

or(x+2x)^4=x^4+4x³(2x)+6x²(2x)²+4x(2x)³+(2x)^4

=x^4+8x^4+24x^4+32x^4+16x^4

=81x^4

d.

(x-y)^4=x^4+4x³(-y)+6x²(-y)²+4x(-y)³+(-y)^4

=x^4-4x³y+6x²y²-4xy³+y^4

e.

(x-2xy)^4=x^4+4x³(-2xy)+6x²(-2xy)²+4x(-2xy)³+(-2xy)^4

=x^4-8x^4y+24x^4y²-32x^4y³+16x^4y^4

=x^4(1-8y+24y²-32y3+16y^4)

Answer 2

a) x⁴+4x³y+6x²y²+4xy³+y⁴

b) x⁴+8x³y+24x²y²+32xy³+16y⁴

c) 81x⁴

d) x⁴-4x³y+6x²y²-4xy³+y⁴

e) x⁴(1 - 8y + 24y²-32y³+16y⁴)

Explanation:

The Binomial theorem describes the algebraic expression of powers of a binomial, it gives us a formula for a binomial of the kind (x ± y)ⁿ, the expansion of the binomial has terms of the form
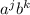`a^jb^k` where j + k = n, and the coefficients of each term are expressed in terms of combinations nCr (remember that nCr are the numbers of ways we can take r elements from a set of n elements where the order doesn't matter) where r ≤ n and r starts being 0 and it keeps growing until reaching n

The formula is

`(x+y)^n= nC0x^ny^0+nC1x^(n-1)y^1 +nC2x^(n-2)y^2+...+nC(n-1)x^1y^(n-1)+nCnx0y^n`)

Now we're going to use this formula for the 4th power of the binomials.

The general formula in this case would be:

`(x+y)^4=4C0x^4y^0+$4C1x^3y^1 +4C2x^2y^2+4C3x^1y^3+4C4x^0y^4\\(x+y)^4=x^4+4x^3y+6x^2y^2+4xy^3+y^4`

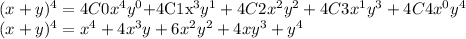
So now we're going to apply the formula for:

a) (x+y)⁴

In this case we can see that this is the general formula as it was written before:

x⁴+4x³y+6x²y²+4xy³+y⁴

b) (x+2y)⁴

In this one we're going to use the formula but x = x and y = 2y

x⁴+4x³(2y)+6x²(2y)²+4x(2y)³+(2y)⁴

=x⁴+8x³y+6x²(4y²)+4x(8y³)+16y⁴

=x⁴+8x³y+24x²y²+32xy³+16y⁴

c)(x+2x)⁴

In this one we're going to use the first x as x and the y = 2x

x⁴+4x³(2x)+6x²(2x)²+4x(2x)³+(2x)⁴

=x⁴+8x⁴+24x⁴+32x⁴+16x⁴

=81x⁴

d) (x-y)⁴

This will be the same as (x + y)⁴but we're going to intercalate the "-" sign, so we get:

x⁴-4x³y+6x²y²-4xy³+y⁴

e) (x-2xy)⁴

For this one we have x = x and y = -2xy in the formula

x⁴-4x³(2xy) + 6x²(2xy)²-4x(2xy)³+(2xy)⁴

=x⁴-8x⁴y+24x⁴y²-32x⁴y³+16x⁴y⁴ we can factorize the x⁴ and we get:

x⁴(1 - 8y + 24y²-32y³+16y⁴)