Answer:
Each side of the square as a lenght of
 units.
units.
The diagonal length is
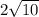 units.
units.
Explanation:
In the image attached, you can observe that one leg of the right triangle has the same length than a side of the square below, that means we need to find that leg length.
Using Pytagorean's Theorem, we have
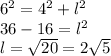
Therefore, each side of the square as a lenght of
 units.
units.
Now, notice that the right triangle inside the square has its hypothesus congruent with the diagonal, using the lengt of each side of the square, we can find the diagonal length.
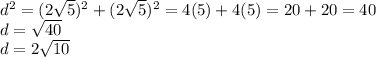
Therefore, the diagonal length is
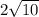 units.
units.