Answer:
Length of the arc = 1146.49 inches
Explanation:
Here, area of the sector = 50 sq inch
Radius = 5 in
Let the angle made by sector on the center = Ф
Now, area of the sector that makes an angle Ф :
Area =
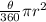
or,
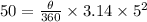
⇒
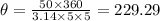
hence, the angle subtended by the arc at the center is Ф = 229.29°
And the length of the arc = Фr
So, arc length = 229. 29 x 5 = 1146.49 inches