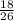Question

A game involves selecting a card from a regular 52-card deck and tossing a coin. The coin is a fair coin and is equally likely to land on heads or tails. You pay $3 to play each round. The random variable X is the Net Earnings when you play the game. • If the card is a Face card, and the coin lands on Heads, you win $9. • If the card is a Face card, and the coin lands on Tails, you win $6. • If the card is not a Face card, you win nothing, no matter what the coin shows. a. How can you find the probability of the value of X = when a Face card is chosen from the deck and a Heads is tossed on the coin?

Answer 1

To find the probability of the value of X when a face card is chosen from the deck and a heads is tossed on the coin, calculate the probability of both events happening

Step-by-step explanation:

The random variable X represents the net earnings when you play the game. To find the probability of the value of X when a face card is chosen from the deck and a heads is tossed on the coin, we need to calculate the probability of both events happening.

The probability of drawing a face card from a standard 52-card deck is 12/52, since there are 12 face cards. The probability of flipping heads on a fair coin is 1/2. Multiplying these probabilities together, we get (12/52) * (1/2) = 3/52.

Therefore, the probability of the value of X being when a face card is chosen from the deck and a heads is tossed on the coin is 3/52.

Answer 2

Expected net earning X for this case is
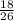`(18)/(26)` =$0.6923

Step-by-step explanation:

We need to calculate the probability of the case and multiply by the net earning. The Case is:

the card is a Face card, and the coin lands on Heads:

Net earning = 9-3 =6

There are 12 Face Cards in a regular 52-card deck. Then,

Probability of a Face Card=
`(12)/(52)`

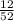
Probability that the coin lands on Tails =
`(1)/(2)`

Then total probability of the case is =
`(12)/(52)` ×
`(1)/(2)` =
`(3)/(26)`

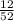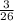
Expected net earning X for this case is =
`(3)/(26)` × 6 =
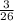`(18)/(26)`