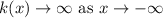Answer:
End behavior of a polynomial function depended on the degree and its leading coefficient.
1. If degree is even and leading coefficient is positive then

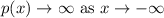
2. If degree is even and leading coefficient is negative then
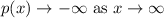
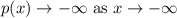
3. If degree is odd and leading coefficient is positive then

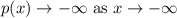
4. If degree is odd and leading coefficient is negative then
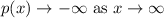
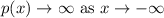
(a)
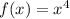
Here, degree is even and leading coefficient is positive.

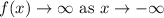
(b)
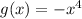
Here, degree is even and leading coefficient is negative.
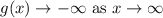
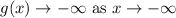
(c)
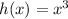
Here, degree is odd and leading coefficient is positive.
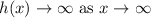
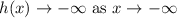
(d)
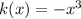
Here, degree is odd and leading coefficient is negative.