Question

A farm supply store carries 50 pound bags of both green pellets and green mash for pig feed. It can store 600 bags of pig feed. At least twice as many of its customers prefer the mash to the pellets. The store buys the pallets for $3.75 per bag and sells them for $6.00. it buys the mash for $2.50 Per bag and sells it for four dollars. If the store orders no more than $1400 worth of pig feed how many bags of mash at the store order to make the most profit

Answer 1

Profit

Explanation:

First we look at the earnings for each of the products, like this:

Grain gain is given by,

$ 3.75 per bag and sells them for $ 6.00, this means a profit equal to $ 6.00 - $ 3.75 = $ 2.25.

Pellets_Profit = $ 2.25

Now we can see the gain in mash, which is equal to $ 4.00− $ 2.50 = $ 1.5.

Mash_ Profit = $ 1.5

The key to the problem is to understand that the maximum benefit will be obtained when a store meets consumer demand. In the best and most positive case, if 2 out of three customers want mash, then it is reasonable that maximum profits are obtained, that is, when the store has 2 bags of mash for every 1 bag of pellets. Applying this to mash and pellets we have the equation,

`2.5 * (2)/(3) x + 3.75*(1)/(3)x = 1400` (1)

Simplifying, that is, multiplying both sides of the equation by 3

`5x + 3.75x = 4200`

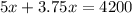
Leaving everything in terms of x and performing the operations

`x = 480`

This is the total number of bags to order, as we noted earlier, 2/3 of the bags must be mashed and 1/3 of pellets, so you must order,

`480* 2/3=320` mash bags and

`480* 1/3=160` pellets bags.

We can also calculate the percentage of profit like this,

160 * $ 3.75 = $ 600 from pellets bags und

320 * $ 2.5 = $ 800 from mash bags.