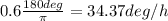Answer:
The answer is
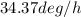 .
.
Explanation:
Use the image provided here for clarification purposes. It helps so much to make a drawing in this sort of questions. The tracking angle here is drawn as
 .
.
Law of sines is applied to the vertical side (ship's trayectory) and the horizontal side (shore line). Here, time must be expressed in hours:
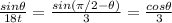
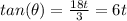 .
.
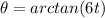 .
.
So, the rate of change of our tracking angle,
 , can be obtained by deriving this expression:
, can be obtained by deriving this expression:
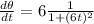 .
.
At 12:30 PM, i.e., half an hour after departure, t = 1/2, so:
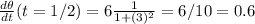 rads/h.
rads/h.
Please note this is the actual rate of change of the tracking angle at this very moment, but not for the rest of moments. It is a function, variable with time, applied to a specific instant. For a value in degrees,