Question

Sketch the graph of each rational function showing all the key features. Verify your graph by graphing the function on

the graphing calculator.
8. f(x) = x2 − 9x/ x

Answer 1

The function is not defined for x=0, so the given function has no y-intercept.

x-intercept of the function is 9.

The function has no vertical or horizontal asymptote.

The function has whole at x=0.

Explanation:

The given function is

`f(x)=(x^2-9x)/(x)`

`f(x)=(x^2)/(x)-(9x)/(x)`

`f(x)=x-9`

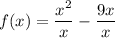
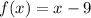
It is a linear function and graph of a linear function is a straight line.

The function is not defined for x=0, so the given function has no y-intercept.

Substitute f(x)=0 to find the x-intercept.

`0=x-9`

`9=x`

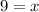
x-intercept of the function is 9.

At x=1,

`f(1)=1-9=-8`

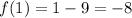
Connect (9,0) and (1,-8) by a straight line.

After cancellation, the given function is a linear function. So, the function has no vertical or horizontal asymptote.

Equate the cancelled factor equal to 0, to find the whole.

`x=0`

Therefore, the function has whole at x=0.