Question

What are the fourth roots of unity in rectangular and polar form? Solve this problem by creating and solving a

polynomial equation. Show work to support your answer.

Answer 1

`\sqrt[4]{1} ={(1,i,-1,-i)`

`\sqrt[4]{1} ={(1\angle0,1\angle90,1\angle180,\angle270)`

Explanation:

The polynomial equation that leads to the fourth roots of unity is the following:

`x^4+1=0`

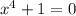
This equation has as solutions the actual roots of the polynom
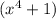`(x^4+1)`, whose roots are, in fact, the routh roots of unity (unity here is the zero-degree term of the polynom).

In rectangular form, the four solutions (roots) are:

`\sqrt[4]{1} ={(1,i,-1,-i)`

Notice that all of them satisfy the equation
`x^4+1=0`.

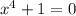In polar form (
`argument \angle angle`):

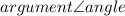`\sqrt[4]{1} ={(1\angle 0 \degree,1\angle90\degree,1\angle180\degree,\angle270\degree)`