Question

To understand the meaning and possible applications of the work-energy theorem. In this problem, you will use your prior knowledge to derive one of the most important relationships in mechanics: the work-energy theorem. We will start with a special case: a particle of mass m moving in the x direction at constant acceleration a. During a certain interval of time, the particle accelerates from vi to vf, undergoing displacement s given by s=xf−xi.

Answer 1

Step-by-step explanation:

The particle travels between two positions
`x_i` and
`x_f`, this can be considered as the result of adding infinite elementary displacements. Therefore, the total work done by force in this displacement is given by:

`W=\int\limits^(x_f)_(x_i) {F\cdot} \, dx`

According to Newton's second law:

`F=ma=m(dv)/(dt)`

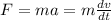
Recall that
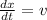`(dx)/(dt)=v` and
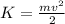`K=(mv^2)/(2)`. So, we have:

`W=\int\limits^(x_f)_(x_i) {ma\cdot} \, dx\\W=m\int\limits^(x_f)_(x_i) {(dv)/(dt)\cdot} \, dx\\W=m\int\limits^(v_f)_(v_i) {v\cdot} \, dv\\\\W=m[(v_f^2)/(2)-(v_i^2)/(2)]\\\\W=K_f-K_i\\W=\Delta K`