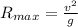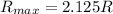Question

A rock is thrown upward from the level ground in such a way that the maximum height of its flight is equal to its horizontal range R. In terms of the original range Rmax, what is the range Rmax the rock can attain if it is launched at the same speed but at the optimal angle for maximum range?

Answer 1

`R_(max) = 2.125 R`

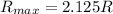
Step-by-step explanation:

If the maximum height attained by the rock is equal to the range of the rock

then we will say

`H = R`

`(v^2 sin^2\theta)/(2g) = (v^2 sin(2\theta))/(g)`

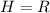
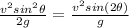
so from this we can say

`(sin^2\theta)/(2) = 2sin\theta cos\theta`

`tan\theta = 4`

`\theta = 75.96 degree`

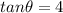
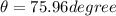
now original range is given as

`R = (v^2 sin(2\theta))/(g)`

`R = (v^2 sin(2* 75.96))/(g)`

`R = 0.47(v^2)/(g)`

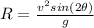
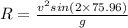
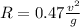
now we know that for maximum possible range we need to throw at 45 degree

`R_(max) = (v^2 sin(2* 45))/(g)`

`R_(max) = (v^2)/(g)`

`R_(max) = 2.125 R`