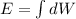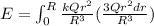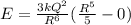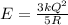Question

A sphere of radius R contains charge Q spread uniformly throughout its volume. Find an expression for the electrostatic energy contained within the sphere itself.

Answer 1

`E = (3kQ^2)/(5R)`

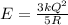
Step-by-step explanation:

Let the sphere is uniformly charge to radius "r" and due to this charged sphere the electric potential on its surface is given as

`V = (kq)/(r)`

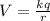
now we can say that

`q = (Q)/((4)/(3)\pi R^3) ((4)/(3)\pi r^3)`

`q = (Qr^3)/(R^3)`

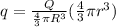
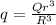
now electric potential is given as

`V = (k(Qr^3)/(R^3))/(r)`

`V = (kQr^2)/(R^3)`

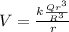
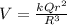
now work done to bring a small charge from infinite to the surface of this sphere is given as

`dW = V dq`

`dW = (kQr^2)/(R^3) dq`

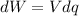
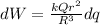
here we know that

`dq = (3Qr^2dr)/(R^3)`

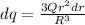
now the total energy of the sphere is given as

`E = \int dW`

`E = \int_0^R  (kQr^2)/(R^3) ((3Qr^2dr)/(R^3))`

`E = (3kQ^2)/(R^6) ((R^5)/(5) - 0)`

`E = (3kQ^2)/(5R)`