Question

A survey found that​ women's heights are normally distributed with mean

63.9

63.9 in and standard deviation

2.4

2.4 in. A branch of the military requires​ women's heights to be between 58 in and 80 in.

a. Find the percentage of women meeting the height requirement. Are many women being denied the opportunity to join this branch of the military because they are too short or too​ tall?

b. If this branch of the military changes the height requirements so that all women are eligible except the shortest​ 1% and the tallest​ 2%, what are the new height​ requirements?


a. The percentage of women who meet the height requirement is


nothing

​%.

​(Round to two decimal places as​ needed.)

Answer 1

a. 99.30% of the woman meet the height requirement

b. If all women are eligible except the shortest​ 1% and the tallest​ 2%, then height should be between 58.32 and 68.83

Step-by-step explanation:

According to the survey, women's heights are normally distributed with mean 63.9 and standard deviation 2.4

a)

A branch of the military requires​ women's heights to be between 58 in and 80 in. We need to find the probabilities that heights fall between 58 in and 80 in in this distribution. We need to find z-scores of the values 58 in and 80 in. Z-score shows how many standard deviations far are the values from the mean. Therefore they subtracted from the mean and divided by the standard deviation:

z-score of 58 in=
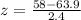`z=(58-63.9)/(2.4)` = -2.458

z-score of 80 in=
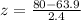`z=(80-63.9)/(2.4)` = 6.708

In normal distribution 99.3% of the values have higher z-score than -2.458

0% of the values have higher z-score than 6.708. Therefore 99.3% of the woman meet the height requirement.

b)

To find the height requirement so that all women are eligible except the shortest​ 1% and the tallest​ 2%, we need to find the boundary z-score of the

shortest​ 1% and the tallest​ 2%. Thus, upper bound for z-score has to be 2.054 and lower bound is -2.326

Corresponding heights (H) can be found using the formula

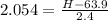`2.054=(H-63.9)/(2.4)` and

`-2.326=(H-63.9)/(2.4)`

Thus lower bound for height is 58.32 and

Upper bound for height is 68.83