Question

A piston with a volume of 847.1 mL is filled with 0.187 moles of a gas at 357.8 K and 305.7 mm Hg. The piston is then compressed by 228.1 mL and cooled to 205.2 K. What is the pressure (in atm) of the piston under these final conditions?

Answer 1

Step-by-step explanation:

p(i)*v(i)/t(i)=p(f)*v(f)/t(f)

plug and chug

Answer 2

Answer : The pressure (in atm) of the piston under these final conditions is, 0.857 atm

Explanation :

Combined gas law is the combination of Boyle's law, Charles's law and Gay-Lussac's law.

The combined gas equation is,

`(P_1V_1)/(T_1)=(P_2V_2)/(T_2)`

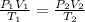
where,

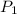`P_1` = initial pressure of gas = 305.7 mmHg

`P_2` = final pressure of gas = ?

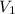`V_1` = initial volume of gas = 847.1 mL

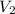`V_2` = final volume of gas = 228.1 mL

`T_1` = initial temperature of gas = 357.8 K

`T_2` = final temperature of gas = 205.2 K

Now put all the given values in the above equation, we get:

`(305.7mmHg* 847.1mL)/(357.8K)=(P_2* 228.1mL)/(205.2K)`

`P_2=651.1mmHg=0.857atm`

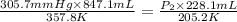
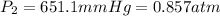
conversion used : (1 atm = 760 mmHg)

Thus, the pressure (in atm) of the piston under these final conditions is, 0.857 atm