Question

Adult male heights have a normal probability distribution with a mean of 70 inches and a standard deviation of 4 inches.

What is the probability that a randomly selected male is more than 74 inches tall?

Answer 1

Answer: 0.1587

Explanation:

Given : Adult male heights have a normal probability distribution with a mean of 70 inches and a standard deviation of 4 inches.

i.e.
`\mu=70 ,\ \sigma=4`

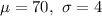
Let x be the random variable that represents the heights of adult males.

Also,
`z=(x-\mu)/(\sigma)`

For x= 74 , we have

`z=(74-70)/(4)=1`

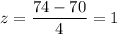
Then, the probability that a randomly selected male is more than 74 inches tall:-

`P(x>74)=P(z>1)=1-P(z\leq1)\\\\=1- 0.8413447\\\\=0.1586553\\\\\approx0.1587` [using z-value table.]

Hence, the probability that a randomly selected male is more than 74 inches tall = 0.1587