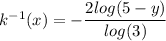Answer:
a.
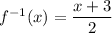
b.
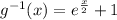
c.
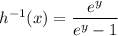
d.
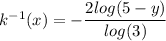
Explanation:
Here is the procediment for each case.
a.
 as we know
as we know
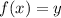 then
then
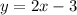 finding the expresion of x, we find the inverse of the function, then:
finding the expresion of x, we find the inverse of the function, then:
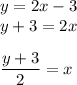
Then:
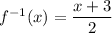
b.
 for this we have to remember that the inverse function of the log is the exp, then:
for this we have to remember that the inverse function of the log is the exp, then:
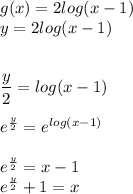
Then the inverse function is:
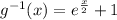
c. In this case we have to also remember the relation between the e and the ln, then:
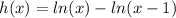 with the properties of the ln we have:
with the properties of the ln we have:
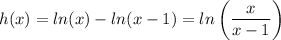 now finding the inverse function we have:
now finding the inverse function we have:
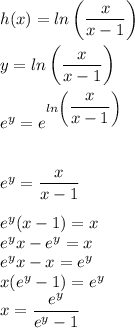
then:
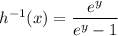
d. in the last one we have:
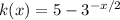 then:
then:
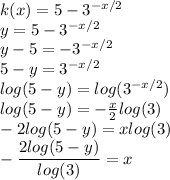
then: