Question

Sketch the graph of each rational function showing all the key features. Verify your graph by graphing the function on

the graphing calculator.
1. f(x) = 4x − 6 / 2x + 5

Answer 1

The Answer is:

Domain of the function: Dom= {x ∈ R: x ≠
`(-5)/(2)`}

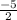Horizontal asymptote: y=2

Vertical asymptote: x=
`(-5)/(2)`

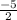
Cut with X-axis: x=
`(-6)/(5)`

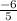
Explanation:

1. Domain of the function: To find the domain of the function you have to find where the dominator of the function is ZERO, so you have to make 2x+5=0

2x+5=0

2x=-5

x=-5/2 Thats the point of the graph that does NOT exist

The domain of the function is: all real numbers except (-5/2) Dom= {x ∈ R: x ≠
`(-5)/(2)`}

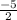2. Horizontal asymptote: take the first numbers that are with the X's in this case:

4x− 6/ 2x+5 you have to take 4x and 2x so y=4/2

3. Vertical asymptote: take the number of 1. and thats the vertical asymptote in this case is x=-5/2

4. Cut with X-axis: replace the x by zero, f(0) = 4(0) − 6 / 2(0) + 5

f(0)=-6/5, f(x)=-6/5

this are the key features of the graph now you can replace numbers and draw your graph