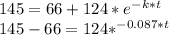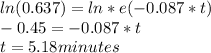Question

Newton's law of cooling states that the temperature of an object changes at a rate proportional to the difference between its temperature and that of its surroundings. Suppose that the temperature of a cup of coffee obeys Newton's law of cooling. If the coffee has a temperature of 190 degrees Fahrenheit when freshly poured, and 2 minutes later has cooled to 170 degrees in a room at 66 degrees, determine when the coffee reaches a temperature of 145 degrees.

Answer 1

5:18

Explanation:

Answer 2

t=5.18 minute

Explanation:

Using Newton's law of cooling

`(dT)/(dt)=-k(T-T_(s))`

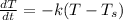
T is temperature of a cup of coffee at any time t
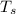`T_(s)`, is the temperature of the surrounding and k is a constant of proportionality in this negative because temperature is decreasing.

`T(0)=190\\T(1)=170\\T_(s)=66`

`(dT)/(dt)=-k(T-T_(s))\\(dT)/((T-T_(s)))=-k*dt\\\int\limits {(1)/(T-T_(s) ) } \, dT=-\int\limits {k} \, dt\\ln(T-T_(s))=k*t+C\\e*ln(T-T_(s))=e^(k*t+C) \\T-T_(s)=e^(k*t)*e^(C)\\e^(C)=C\\T-T_(s)=e^(k*t)*C\\T=T_(s)+e^(k*t)*C`

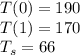
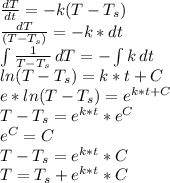
To find constant knowing the time and the temperature the first step of the change of energy in cup of coffee

`T=T_(s) +e^(-k*t)*C\\ C=190-66=124\\170=66+124*e^(-k*2)\\ 170-66=124*e^(-k*2)\\ln((104)/(124))=ln*e^(-k*2)\\-0.175=-k*2\\k=0.08794`

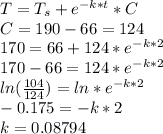
Now using the constant of decreasing can find the time to be a 145 temperature the cup of coffee

`145=66+124*e^(-k*t) \\145-66=124*^(-0.087*t)`

`ln(0.637)=ln*e(-0.087*t)\\-0.45=-0.087*t\\t=5.18minutes`