Question

Explain how Pascal’s triangle allows you to compute the coefficient of x2y3 when (x − y)5 is

expanded

Answer 1

-10

Explanation:

Pascal’s triangle: It represents the binomial coefficients. If a binomial expression is (a+b)^n, then (n+1)th row of Pascal’s triangle represents the binomial coefficients or that binomial expression.

The given binomial expression is

`(x-y)^5`

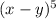
The elements of 6th row are 1, 5, 10, 10, 5 and 1.

`(x-y)^5=1(x)^5+5(x)^4(-y)^1+10(x)^3(-y)^2+10(x)^2(-y)^3+5(x)^1(-y)^4+1(-y)^5`

`(x-y)^5=x^5 - 5 x^4 y + 10 x^3 y^2 - 10 x^2 y^3 + 5 x y^4 - y^5`

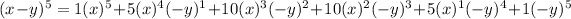
Therefore, the coefficient of x²y³ is -10.