Question

Sketch the graph of each rational function showing all the key features. Verify your graph by graphing the function on

the graphing calculator.
2. f(x) = (3x − 6)(x − 4) / x(x − 4)

Answer 1

The x-intercept is 2.

The function has no y-intercept.

The vertical asymptote of the function is x=0.

The horizontal asymptote of the function is x=0.

The function has hole at x=4.

Explanation:

The given function is

`f\left(x\right)=((3x-6)(x-4))/(x(x-4))`

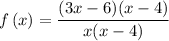
Cancel out common factors.

`f\left(x\right)=(3x-6)/(x)`

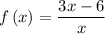
(i) x-intercept.

Substitute f(x)=0, in the given function.

`0=(3x-6)/(x)`

`0=3x-6`

`-3x=-6`

`x=2`

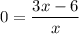
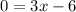
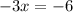
The x-intercept is 2.

(i) y-intercept.

Substitute x=0, in the given function.

`f\left(x\right)=(3(0)-6)/((0))=\infty`

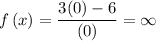
The function has no y-intercept.

(iii) Vertical asymptote.

Equate the denominator equal to 0.

`x=0`

Therefore, the vertical asymptote of the function is x=0.

(iv) Horizontal asymptote.

If degree of numerator and denominator are same, then horizontal asymptote is

`y=\frac{\text{Leading coefficient of numerator}}{\text{Leading coefficient of denominator}}`

`y=(3)/(1)`

`y=3`

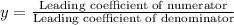
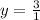
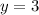
Therefore, the horizontal asymptote of the function is x=0.

(v) End behavior

`f(x)\rightarrow 3\text{ as }x\rightarrow -\infty`

`f(x)\rightarrow \infty\text{ as }\rightarrow 0^(-)`

`f(x)\rightarrow -\infty\text{ as }\rightarrow 0^(+)`

`f(x)\rightarrow 3\text{ as }\rightarrow \infty`

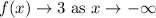
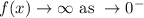
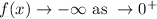
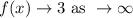
(vi) holes

Equate the cancel factors equal to 0, to find the holes.

`x-4=0`

`x=4`

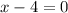
The function has hole at x=4.