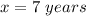Answer:
Part a)
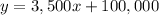
Part b)
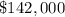
Part c)

Explanation:
Part a) Find the equation that models the value of the house in y dollars after x years
we know that
The linear equation in slope intercept form is equal to

where
m is the rate or slope
b is the y-coordinate of the y-intercept (initial value)
Let
x -----> the number of years
y ----> the value of the house in dollars
In this problem we have

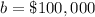
substitute
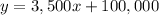
Part b) Find the value of the house in 12 years.
so
For x=12 years
substitute in the equation and solve for y
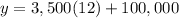
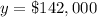
Part c) How many years from now will the value of the house be $124,500?
For y=$124,500
substitute in the equation and solve for x
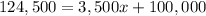
subtract 100,000 both sides
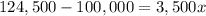
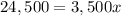
Divide by 3,500 both sides